How Many Seconds Will It Take a Bus That Is Traveling at a Constant Speed of 80 Km/hr

I-Dimensional Kinematics Review

Navigate to:

Review Session Dwelling house - Topic Listing

1D Kinematics - Domicile || Printable Version || Questions and Links

Answers to Questions:  #1-seven || #8-#28 || #29-#42 || #43-#50

[ #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 ]

Part E: Computational Problems

43. Determine the acceleration (in m/s²) of an object which ... .

1. moves in a straight line with a constant speed of xx.0 m/south for 12.0 seconds
2. changes its velocity from 12.1 m/s to 23.v m/due south in 7.81 seconds
3. changes its velocity from 0.0 mi/hr to 60.0 mi/hour in iv.20 seconds
4. accelerates from 33.iv thousand/s to eighteen.9 m/due south over a distance of 109 m

Answer: See answers, explanations and calculations below.

a. If the speed and direction of an object is constant, so the acceleration is 0 thousand/s² .

b. The dispatch is the velocity alter per time ratio:

a = (Velocity Change)/t = (23.5 m/s - 12.ane m/s) / (7.81 s) = 1.46 m/s^two .

c. The dispatch is the velocity modify per time ratio:

a = (Velocity Change)/t = (60.0 mi/hr - 0.0 mi/hr) / (iv.twenty s) = xiv.3 mi/hr/s.

14.iii mi/hr/south * (1.0 thousand/s) / (2.24 mi/hour) = 6.38 yard/southward² .

d. The acceleration value can also be calculated using kinematic equations if three other kinematic quantities are known. In this instance, the know information is: v_o = 33.four m/s; v_f = eighteen.ix m/s; and d = 109 k. Using the equation v_f ^two = v_o ² + ii*a*d, the acceleration can be computed.

a = (v_f ² - five_o ²) / (ii*d) = [(eighteen.9 m/s)^two - (33.4 m/s)² ] / (ii * 109 m) = -three.48 m/s² . [ #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 ]

44. Decide the magnitude of the displacement (in meters) of an object which ... .

1. moves from Hither to Yon (with an average speed of 28.0 m/southward) and then back to Hither (with an average speed of 28.0 yard/due south) if both the forward and the return trip take 46 minutes each.
2. moves at a constant speed of 8.30 m/s in a directly line for 15.0 seconds.
3. decelerates at a charge per unit of -4.35 m/due south/south from a speed of 38.i k/southward to a speed of 17.6 m/south
4. accelerates from rest at a rate of 3.67 m/s² for 12.1 seconds
5. is moving at 12.2 m/s and so accelerates at a rate of +ane.88 m/s² for 17.0 seconds

Answer: See answers, explanations and calculations beneath.

a. Since this is a round-trip journey, the overall deportation is 0 m.

b. Since the velocity is constant, the displacement can be constitute by multiplying the velocity by the fourth dimension.

d = 5*t = (viii.xxx k/southward) * (15.0 due south) =125 m

c. A displacement value tin can likewise exist calculated using kinematic equations if 3 other kinematic quantities are known. In this case, the know information is: v_o = 38.ane g/s; v_f = 17.6 one thousand/s; and a = -4.35 chiliad/s/s. Using the equation v_f ² = five_o ^two + ii*a*d, the deportation can be computed.

d = (v_f ² - v_o ²) / (ii*a) = [(17.six one thousand/due south)^two - (38.1 thousand/southward)² ] / (2 * -4.35 g/s/s) = 131 m.

d. A displacement value can be calculated using other kinematic equations if a unlike prepare of kinematic quantities is known. Here we know that: v_o = 0.0 m/s; t = 12.one s; and a = 3.67 m/s/south. Using the equation d = v_o* t + 0.5*a*t², the displacement can be computed.

d = (0 m/s)*(12.i s) + 0.5*(3.67 k/s/s)*(12.i s)² = 269 yard.

eastward. Here the displacement value is calculated using the same kinematic equation. We know that: five_o = 12.2 m/s; t = 17.0 s; and a = 1.88 m/due south/s. Using the equation d = v_o* t + 0.five*a*t^two, the displacement can be computed.

d = (12.2 m/south)*(17.0 due south) + 0.v*(1.88 m/due south/s)*(17.0 s)² = 479 m. [ #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 ]

45. The hare is sleeping at a location that is 1200 m from the finish line. The tortoise passes him at a steady speed of v.0 cm/s. If the hare finally wakes up 6.5 hours later, then what minimum dispatch (causeless constant) must he have in club to pass the tortoise earlier the finish line.

Answer: 0.0067 g/s²

Like a lot of physics word bug, at that place is more than one path to the terminal answer. In all such issues, the solution involves thought and good problem-solving strategies (describe a picture, list what you know, list pertinent equations, etc.).

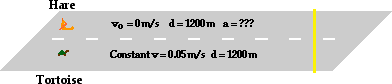
The tortoise, moving at a constant speed, will comprehend the 1200 m in a time of:

t_tortoise = d/five_tortoise = (1200 1000) / (0.050 m/s) = 24000 south = half dozen.666... hrs

The hare volition sleep for half-dozen.5 hrs (23400 s) before starting, and then volition have only 0.1666... hrs (600 s) to accelerate to the terminate line. So the acceleration of the hare can exist make up one's mind using a kinematic equation. The know data about the hare'due south motion is: t = 600 due south; d = 1200 m; v_o = 0 1000/south. The best equation is d = v_o* t + 0.5*a*t². The 5_o* t term cancels and the equation can be algebraically rearranged and solved for a:

a = two*d / t² = ii * (1200 m) / (600 due south)² = 0.0067 m/southward². [ #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 ]

46. A Gold Car moving at 12.0 m/s passes a Green Car while the Green Car is at rest at a stoplight. The Dark-green Machine immediately accelerates at a rate of +i.fourscore m/s/due south for 11.0 seconds seconds and and then maintains a abiding speed. After how much time (relative to the initial starting fourth dimension) must the Green Motorcar bulldoze earlier catching up with the Gold Motorcar .

Respond: 14.0 s

(As mentioned in the previous problem ...) Like a lot of physics give-and-take bug, there is more than one path to the concluding answer. In all such problems, the solution involves thought and good problem-solving strategies (draw a picture, list what you lot know, list pertinent equations, etc.).

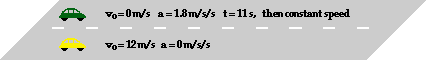
Here the golden car travels with a abiding speed for a time of t seconds (where t is the full time of travel for both cars). The altitude traveled past the gilt automobile is given by the kinematic equation d = v_o* t + 0.5*a*t². The second term cancels and the distance tin exist expressed as

d = v_o* t + 0.5*a*tⁱⁱ = (12.0 m/due south)*t, or

d_gold = 12.0* t

For the dark-green car, there is an accelerated period and and so a abiding speed period. The distance traveled during the accelerated period (d_1green) is institute from the same kinematic equation. For the green auto, the first term cancels and the distance is

d_1green = 5_o* t + 0.5*a*t² = 0.5*(1.lxxx m/south²)*(11.0 southward)², or

d_1green = 108.9 one thousand

Once the green automobile has accelerated for eleven seconds, it maintains a constant speed for the remaining time, given by the expression t - 11 due south. The speed at which the greenish car is traveling during this time can be computed using the equation:

5_fgreen = v_o + a*t = (1.80 m/s²) *(xi.0 s) = 19.8 grand/s

The distance traveled by the green motorcar during this abiding speed portion of its motion (d_2green) can be computed using the kinematic equation. d = v_o* t + 0.5*a*t². The second term cancels and the altitude tin be expressed as

d_2green = v_o* t + 0.v*a*t² = (19.viii m/southward) * (t - xi s) = 19.8*t - 217.8, or

d_2green = xix.8*t - 217.eight

Then the total distance traveled by the light-green car is given by the expression:

d_green = d_1green + d_2green = 108.9 + 19.8*t - 217.eight

d_green = 19.8*t - 108.9

When the light-green car catches upwardly to the gilded car their distance traveled will be the same. Then the time t can be determined by setting the two expressions for altitude equal to each other and solving for t.

12.0* t = 19.8*t - 108.ix

108.ix = seven.eighty*t

t = (108.9) / (7.80)

t = 13.96 southward = 14.0 southward

[ #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 ]

47. Ima Rilla Saari is cruising at 28.0 m/southward downwardly Lake Artery and through the forest preserve. She notices a deer jump into the road at a location 62.0 m in front of her. Ima get-go reacts to the upshot, then slams on her brakes and decelerates at -8.x m/s², and ultimately stops a picometer in front of the frozen deer. What is Ima's

reaction time ? (i.e., how long did information technology take Ima to react to the event prior to decelerating?)

Answer: 0.486 southward

Ima'south total distance traveled (62.0 grand) tin can be broken into ii segments - a reaction distance (d_rxn) and a braking distance (d_braking). The reaction distance is the altitude Ima moves prior to braking; she will move at constant speed during this fourth dimension of t_rxn . The braking distance is the distance which Ima moves when her foot is on the brake and she decelerates from 28.0 m/south to 0.0 chiliad/due south. The braking distance can be computed showtime using the post-obit kinematic equation: v_f ⁱⁱ = v_o ² + 2*a*d. The known information for this braking period is: v_o = 28 g/s; five_f = 0 m/due south; and a = -eight.10 m/south/south. The substitutions and solution are shown below.

d_braking = (5_f ² - 5_o ²) / (2*a) = [(0 m/south)ⁱⁱ - (28.0 m/s)ⁱⁱ ] / (2 * -8.10 m/s/s) = 48.40 grand.

Since Ima'due south car requires 48.40 m to brake, she can travel a maximum of thirteen.6 m during the reaction catamenia. The relationship between reaction time, speed and reaction distance is given by the equation

d_rxn = v * t_rxn

Substituting 13.6 m for d_rxn and 28.0 m/s for v, the reaction time tin can be computed:

t_rxn = (13.6 k) / (28.0 1000/s) = 0.486 s [ #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 ]

48. A ii-phase rocket accelerates from residual at +3.57 m/southward/s for half-dozen.82 seconds. It then accelerates at +ii.98 one thousand/s/s for another 5.90 seconds. After the second stage, it enters into a country of free autumn. Determine:

1. the maximum speed
2. the maximum altitude
3. the height of the rocket after 20.0 seconds
4. the total fourth dimension the rocket is in the air (assuming it is launched from the basis)

Reply: See answers and explanations below.

This problem can be approached past either the use of a velocity-time graph or the apply of kinematic equations (or a combination of each). Whatever the arroyo, it is imperative to break the multistage motion upward into its iii different dispatch periods. The use of kinematic equations is only appropriate for constant acceleration periods. For this reason, the complex motion must be broken upwardly into fourth dimension periods during which the dispatch is abiding. These three time periods can be seen on the velocity-time graph by three lines of distinctly different gradient. The diagram at the right provides a delineation of the move; strategic points are labeled. These points will exist referred to in the solutions below. The velocity-fourth dimension plot below will exist used throughout the solution; notation that the same strategic points are labeled on the plot.

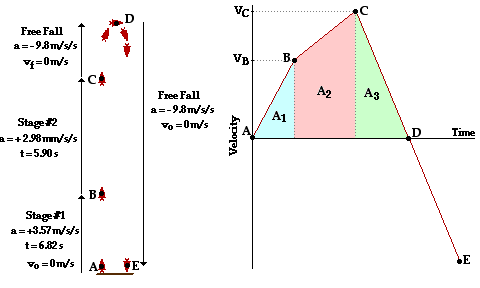
a. The maximum speed occurs after the second stage or dispatch menstruum (signal C). After this time, the upwardly-moving rocket begins to boring downwardly equally gravity becomes the sole strength acting upon it. To determine this speed (v_c), the kinematic equation v_f = 5_o + a*t will be used twice - once for each acceleration period.

Starting time Stage: 5_B = 5_A + a*t = 0 m/south + (3.57 m/s/s) * (six.82 s) = 24.3 1000/s

2d Stage: v_C = v_B + a*t = 24.three m/due south + (2.98 chiliad/southward/due south) * (five.90 s) = 41.ix thou/s

b. The maximum altitude occurs at point D, old afterwards the second stage has ceased and the rocket finally runs out of steam. The velocity at this point is 0 thousand/due south (information technology is at the height of its trajectory). The distance at this point is the cumulative distance traveled from t = 0 s to t = t_D. This distance is the altitude for the first stage, the second stage and the deceleration period (C to D). These distances correspond to the surface area on the five-t graph; they are labeled A₁, A₂, and A₃ on the graph. They are calculated and summed below.

A₁ = 0.5*b*h = 0.5 * (24.iii 1000/s) * (half dozen.82 s) = 82.86 m

A₂ = b*h + 0.5*b*h (a triangle on superlative of a square)

A₂ = (24.iii m/s) * (5.9 s) + 0.5 * (41.9 m/s - 24.3 m/southward) * (v.ix south) = 195.42 chiliad

Information technology will be necessary to know the time from point C to signal D in social club to determine A₃. This time tin can exist determined using the kinematic equation v_f = v_o + a*t for which 5_f = 0 m/south and five_o = 41.9 1000/s and a = -ix.eight m/southward/s.

v_D = v_C + a*t

0 m/southward = 41.nine m/s + (-ix.8 m/s/s) * t

t = 4.28 due south

At present A₃ can be determined using the v-t graph. The surface area is a triangle and is calculated as

A₃ = 0.5*b*h = 0.5 * (41.ix g/due south) * (iv.82 s) = 89.57 m

The maximum altitude is the sum of the three distances (areas)

Max. distance = 82.86 m + 195.42 m + 89.57 m =368 g

c. When the rocket reaches indicate D, the time is 17.0 seconds. The altitude at 20.0 seconds will be the 368 meters risen above the launch pad from point A to signal D minus the distance fallen from the peak from 17.0 to 20.0 seconds. This distance would exist represented by a negative expanse on the velocity-fourth dimension graph. The surface area is a triangle and can be computed if the velocity at twenty seconds is known. It can exist calculated using a kinematic equation and then used to determine the surface area of a triangle. Alternatively, a kinematic equation can be used to decide the altitude fallen during these iii.0 seconds. The work is shown below:

d = five_o* t + 0.5*a*t² = 0.5 * (-9.8 thou/s/s) * (three.0 due south)ⁱⁱ = 44.ane one thousand

The altitude at 20 seconds is therefore the ~369 thousand risen in the beginning 17 seconds minus the ~44 grand fallen in the next 3 seconds. The answer is325 m.

d. The rocket rises 369 m in the beginning 17.0 seconds. In the fourth dimension subsequent of this, the rocket must fall 369 meters. The fourth dimension to fall 369 1000 can be found from the same kinematic equation used in role c.

d = 5_o* t + 0.5*a*t²

-368 yard = 0.5 * (-9.8 m/south/due south) * t²

t = 8.67 seconds

This time can be added onto the 17.0 seconds to decide the time at which the rocket lands:25.7 seconds.

[ #43 | #44 | #45 | #46 | #47 | #48 | #49 | #fifty ]

49. In a 200.0-m relay race (each leg of the race is 50.0 grand long), one swimmer has a 0.450 2d pb and is pond at a constant speed of 3.90 one thousand/s towards the contrary end of the puddle. What minimum speed must the second swimmer have in order to catch up with the first swimmer past the end of the pool?

Reply: four.04 m/s

Both swimmers swim the aforementioned distance (50 m) at constant speed. Swimmer A (who was simply arbitrarily named) gets a 0.450 second head start. So swimmer B must travel faster in order to terminate the race in less fourth dimension than swimmer A. First, the time required of swimmer A to consummate the 50l0 1000 at 3.90 m/s can exist computed. The fourth dimension is

t_A = d/v_A = (50.0 grand) / (iii.90 m/s) = 12.82 s

Thus, swimmer B must end the same 50.0 one thousand in 12.37 seconds (12.82s - 0.45 s). So the speed of swimmer B can be computed every bit

v_B = d/t_B = (l.0 m) / (12.37 s) = 4.04 m/s [ #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 ]

50. A drag racer accelerates from rest at an average rate of +13.2 m/s² for a distance of 100. m. The driver coasts for 0.500 seconds and so uses the brakes and parachute to decelerate until the terminate of the track. If the total length of the track is 180. m, what minimum deceleration charge per unit must the racer accept in order to end prior to the end of the track?

Answer: -24 m/s/s

This problem can be approached past first determining the distance over which the dragster decelerates. This distance will be less than 80. meters by an amount equal to the altitude which the dragster coasts later crossing the terminate line. See diagram.

The distance traveled by the dragster prior to braking is 100 k plus the coasting distance. The benumbed altitude can be determined if the speed of the dragster at the cease of 100 m is adamant. So outset, a kinematic equation will be used to determine the speed and then the benumbed distance will be computed.

Using the equation v_f ² = 5_o ² + 2*a*d, the speed after 100 k can be determined. This exchange and solution is shown below.

five_f ⁱⁱ = v_o ² + two*a*d = two*(13.2 m/s/southward)*(100. thou) = 2640 m²/s²

v_f = 51.4 m/due south

Coasting at 51.38 g/s for 0.500 s will lead to a distance traveled of 25.7 m.

Once the coasting period is over, at that place is a curt distance left to decelerate to a stop. This distance is

180. m - 100. yard - 25.7 m = 54 1000

At present the same kinematic equation can exist used to determine the deceleration rate during the last 54 grand of the track. Known data is: v_o = 51.four m/s; v_f = 0 m/s; and d = 54 thou. Using the equation 5_f ^two = five_o ² + ii*a*d, the acceleration tin can be computed.

a = (five_f ² - v_o ²) / (2*d) = = [(51.4 thousand/s)² - (0 m/s)² ] / (2 * 54 g) = -24 chiliad/s² . [ #43 | #44 | #45 | #46 | #47 | #48 | #49 | #50 ]

Navigate to:

Review Session Home - Topic Listing

1D Kinematics - Home || Printable Version || Questions and Links

Answers to Questions:  #1-seven || #eight-#28 || #29-#42 || #43-#50

You Might As well Like ...

Users of The Review Session are ofttimes looking for learning resources that provide them with exercise and review opportunities that include built-in feedback and instruction. If that is what y'all're looking for, then you lot might also similar the following:

1. The Calculator Pad

   The Calculator Pad includes physics word bug organized by topic. Each problem is accompanied by a pop-up answer and an audio file that explains the details of how to arroyo and solve the problem. It'southward a perfect resource for those wishing to meliorate their trouble-solving skills.

   Visit: The Figurer Pad Home | Reckoner Pad - Kinematics

2. Minds On Physics the App Serial

   Minds On Physics the App ("MOP the App") is a series of interactive questioning modules for the student that is serious about improving their conceptual understanding of physics. Each module of the serial covers a different topic and is further broken down into sub-topics. A "MOP experience" will provide a learner with challenging questions, feedback, and question-specific help in the context of a game-similar environment. It is available for phones, tablets, Chromebooks, and Macintosh computers. It's a perfect resources for those wishing to refine their conceptual reasoning abilities. Part 1 of the serial includes Kinematic Concepts and Kinematic Graphing.

   Visit: MOP the App Abode || MOP the App - Function 1

Share this post